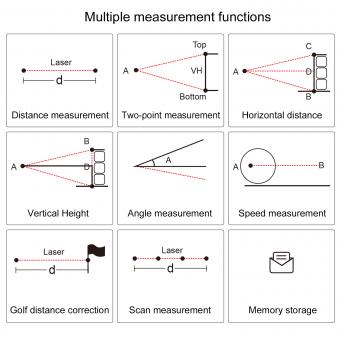
How To Calculate Resolution Microscope ?
The resolution of a microscope can be calculated using the formula:
Resolution = λ / (2 * NA)
Where:
- λ is the wavelength of light used in the microscope
- NA is the numerical aperture of the objective lens
The numerical aperture is a measure of the lens' ability to gather light and resolve fine details. It depends on the refractive index of the medium between the lens and the specimen, as well as the angle of the cone of light entering the lens.
By using a shorter wavelength of light and a higher numerical aperture, the resolution of the microscope can be improved. This allows for the visualization of smaller details in the specimen.
It is important to note that the resolution calculated using this formula represents the theoretical limit of the microscope's resolving power. In practice, other factors such as lens aberrations and specimen preparation can affect the actual resolution achieved.
1、 Numerical aperture
To calculate the resolution of a microscope, one needs to consider the numerical aperture (NA) of the microscope's objective lens. The numerical aperture is a measure of the lens's ability to gather light and resolve fine details. It is determined by the lens's refractive index and the angle of light it can accept.
The resolution of a microscope is given by the formula:
Resolution = λ / (2 * NA)
Where λ is the wavelength of light used in the microscope. This formula is known as the Rayleigh criterion and provides an estimate of the smallest resolvable detail.
In recent years, there have been advancements in microscopy techniques that have pushed the limits of resolution beyond what was previously thought possible. One such technique is super-resolution microscopy, which utilizes fluorescent molecules to overcome the diffraction limit of light. This technique allows for the visualization of structures at the nanoscale level, providing unprecedented detail.
Additionally, advancements in computational imaging have also contributed to improving resolution. By using algorithms and image processing techniques, it is possible to enhance the resolution of images captured by microscopes. This approach, known as computational microscopy, has the potential to further improve the resolution of microscopes without the need for physical modifications.
In conclusion, the resolution of a microscope can be calculated using the numerical aperture of the objective lens and the wavelength of light used. However, recent advancements in super-resolution microscopy and computational imaging have expanded the possibilities for achieving higher resolution and visualizing finer details.

2、 Wavelength of light
To calculate the resolution of a microscope, you need to consider the wavelength of light being used. The resolution of a microscope refers to its ability to distinguish two closely spaced objects as separate entities. The smaller the resolution, the better the microscope's ability to distinguish fine details.
The resolution of a microscope can be calculated using the formula:
Resolution = (0.61 x Wavelength) / Numerical Aperture
The wavelength of light is an important factor in determining the resolution. In traditional light microscopes, visible light with a wavelength of around 400-700 nanometers is used. However, recent advancements in microscopy techniques have allowed the use of shorter wavelength light, such as ultraviolet or even X-rays, which can provide higher resolution.
Using shorter wavelength light can improve the resolution of a microscope because the resolution is inversely proportional to the wavelength. This means that as the wavelength decreases, the resolution increases. Shorter wavelength light allows for better differentiation of closely spaced objects, resulting in higher resolution images.
It is worth noting that the numerical aperture (NA) of the microscope's objective lens also plays a crucial role in determining the resolution. The NA is a measure of the lens's ability to gather light and resolve fine details. Higher NA values result in better resolution.
In conclusion, to calculate the resolution of a microscope, you need to consider the wavelength of light being used and the numerical aperture of the objective lens. Using shorter wavelength light and higher NA values can improve the resolution, allowing for better visualization of fine details in microscopic samples.

3、 Rayleigh criterion
To calculate the resolution of a microscope using the Rayleigh criterion, you need to consider the wavelength of light used and the numerical aperture (NA) of the lens. The Rayleigh criterion states that two point sources can be resolved if the maximum of one Airy disk falls on the first minimum of the other Airy disk.
The formula to calculate the resolution (R) is given by:
R = 0.61 * λ / NA
Where λ is the wavelength of light used and NA is the numerical aperture of the lens. The numerical aperture is a measure of the lens's ability to gather light and is determined by the lens design and the refractive index of the medium between the lens and the specimen.
It is important to note that the Rayleigh criterion assumes ideal conditions and does not take into account factors such as aberrations, scattering, or diffraction. In practice, these factors can limit the resolution of a microscope.
In recent years, there have been advancements in microscopy techniques that have pushed the limits of resolution beyond what was previously thought possible. Techniques such as super-resolution microscopy, including stimulated emission depletion (STED) microscopy and structured illumination microscopy (SIM), have allowed for resolutions beyond the diffraction limit. These techniques use various methods to overcome the diffraction barrier and achieve resolutions on the nanoscale.
Overall, while the Rayleigh criterion provides a basic calculation for resolution, it is important to consider the limitations and advancements in microscopy techniques to fully understand the capabilities of modern microscopes.

4、 Abbe's diffraction limit
To calculate the resolution of a microscope, we can use Abbe's diffraction limit formula. This formula, developed by Ernst Abbe in the late 19th century, provides an estimate of the smallest resolvable detail in a microscope image. The formula is given as:
Resolution = λ / (2 * NA)
Where λ is the wavelength of light used in the microscope and NA is the numerical aperture of the objective lens.
The numerical aperture is a measure of the lens' ability to gather light and resolve fine details. It is determined by the refractive index of the medium between the lens and the specimen, as well as the angle of the cone of light entering the lens. A higher numerical aperture results in a smaller resolution limit.
In recent years, there have been advancements in microscopy techniques that have pushed the limits of resolution beyond what was previously thought possible. Techniques such as super-resolution microscopy, including stimulated emission depletion (STED) microscopy and structured illumination microscopy (SIM), have allowed researchers to achieve resolutions beyond the diffraction limit.
These techniques utilize various methods to overcome the diffraction limit, such as using fluorescent molecules that can be switched on and off, or using patterned illumination to extract high-frequency information from the sample.
It is important to note that while these techniques can achieve resolutions beyond the diffraction limit, they are often limited to specific conditions and may require specialized equipment or sample preparation. Additionally, the resolution achieved may vary depending on the specific microscope setup and the properties of the sample being imaged.
In conclusion, the calculation of resolution in a microscope using Abbe's diffraction limit formula provides a good estimate of the smallest resolvable detail. However, recent advancements in microscopy techniques have allowed for resolutions beyond the diffraction limit, opening up new possibilities for studying biological and physical systems at the nanoscale.